Viper

Verifiable Reinforcement Learning via Policy Extraction

While deep reinforcement learning has been shown to be effective in a variety of domains, it suffers from the same problems as other machine learning methods: it is difficult to interpret and it is difficult to guarantee that it is behaving correctly. In this article, I present my efforts in reproducing the results of the paper "Verifiable Reinforcement Learning via Policy Extraction" by Osbert Bastani et al. In particular, I will answer the following questions:

The code accompanying this article can be found here.

Background

Reinforcement Learning is gaining increasing importance in safety-critical domains, necessitating the ability to verify that the agent is behaving correctly. This is especially important in domains where the agent is interacting with the real world, such as self-driving cars, air traffic control, and robotics. Unlike playing a game of Go, failure in these real-world scenarios can incur significantly higher perhaps even unacceptable costs. So while there are approaches that aim to teach RL agents safe behavior we would optimally like to be able to demonstrate that our agent never fails.

Even though there is work on verifying Deep Reinforcement Learning agents the process is complicated by the complexity of the computation graph of a neural network. Instead, we will first train a Deep RL agent and then distill it into a decision tree (DT) using imitation learning. This decision tree can then be verified using an SAT solver.

Training the oracle

As we will see later for our verification algorithm to work we need to have a functional description of the state dynamics f(s) of our environment. While the authors are also able to verify other properties such as robustness in environments where that is not the case such as Atari Pong, we will here only focus on the Toy Pong environment where we can easily compute the state dynamics.

The environment is a one-player version of the Atari Pong where the player controls a paddle and the opponent is simply a wall. The paddle can move left or right and the ball bounces off the walls and the paddle. The goal is to keep the ball in play for as long as possible. We can describe the state of the environment at timestep t with the following vector:

s_t = (x_p, x_b, y_b, v_x, v_y)
The ToyPong environment at timestep 0

The ball starts at the center of the screen and is initialized with a random velocity in both the x and the y direction with a magnitude between 1 and 2. The paddle starts at the center bottom of the screen and can be controlled via the actions {left, right, stay}. The speed of the paddle is not given, so I initially assumed it to be 1. However, after some experimentation, I quickly learned that this makes the game impossible to play perfectly as there are many cases where the ball is too fast to catch no matter what the controller does. A quick calculation shows that the paddle's speed needs to be at least 1.5.

Having the environment set up we now would like to train an oracle that can play the game perfectly. While the authors used a generic policy gradient for training a DNN policy I decided to go directly for the stable baselines 3 PPO implementation as it is a good starter for Deep RL. Usually it is enough in RL for an agent to achieve a very high reward so training even this state-of-the-art algorithm to play perfectly Here perfectly only means that the agent achieves the highest reward possible (r=250) averaged over 50 rollouts. Unlike the decision tree we are extracting it might still lose given certain edge cases. turned out to be surprisingly difficult. The key hyperparameter that made it work in the end was using a learning rate that would decay linearly after half the training was complete.

🐍 VIPER

One naive way of approaching the distillation challenge would be to train our decision tree to predict the action of the oracle given the states of all trajectories in the training set. This, however, turns out to yield poor results because the decision tree is not able to generalize to unseen states. This is because mo matter how good our action classification accuracy is on the training set, the decision tree will likely end up in a state where it has never seen before. This is especially true for stochastic environments. DAgger is an algorithm that solves this by letting the decision tree play on its own and then retrieving the correct actions from the oracle and adding them to the training set. This process is repeated as often as necessary yielding an ever expanding training set.

The VIPER algorithm is based on DAgger but adds one important insight: Not all states in a game are equally important to its outcome. In the figure below for instance we can see that on the left side, the ball is moving away from the paddle so the next action is not consequential for the overall return. On the right side however it is crucial for the paddle to move to the right in order to keep the ball in play. We can use this insight to weight state action pairs by their importance for the overall return. But how do we know which states are critical and which are not?

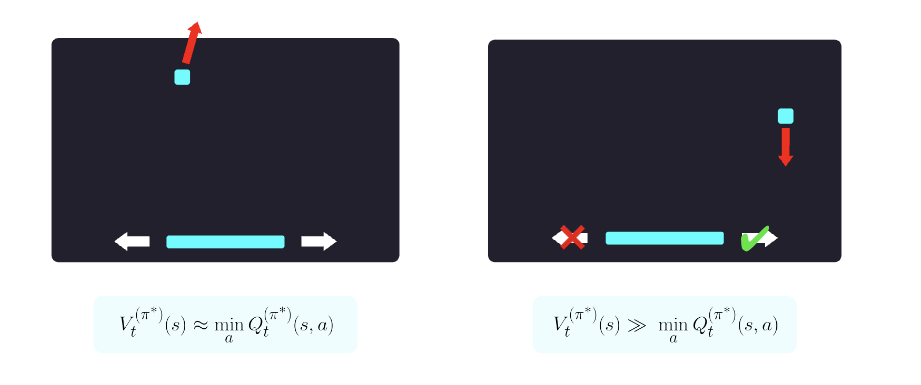
The state on the left is not critical for the overall return while the state on the right is. Adapted from Bastani et al.

For this, we can leverage the Q-function of the oracle \pi^* . Remember: The Q-function is a function that maps a state and an action to the expected return of taking that action in that state. Now suppose we have a set of q-values for a given state and the best possible action has a q-value that is very close to the worst possible action. In that case, we can be pretty sure that the best action is not critical for the overall return because no matter which action we pick the expected return will not change much. On the other hand if the difference is very high then making the wrong choice could have disastrous consequences. We can now use this to weight every sample in our training set with this expression:

The "criticalness" of the state.
\tilde{\ell}(s_t) ~~~=~~~~
[V_t^{(\pi^*)}
~~~-~~~
\min_{a \in A}Q_t^{(\pi^*)}(s, a)]
~~~ \mathbb{I}\left[\pi(s) \neq \pi^*(s)\right]
The maximum q-value
the minimum q-value
the classifier 0-1 loss

The sample weights can be obtained directly from our stable baselines oracle policy like so. Now we have all the components to build and analyze the VIPER algorithm. The code below is a simplified snippet from the repository with comments to explain each step:

dataset = [] policy = None policies = [] rewards = [] for i in range(args.n_iter): # Beta controls if we use the oracle or the decision tree # Use the oracle only for the first iteration beta = 1 if i == 0 else 0 dataset += sample_trajectory(args, policy, beta) # Train a scikit-learn decision tree on the growing dataset clf = DecisionTreeClassifier(ccp_alpha=0.0001, criterion="entropy", max_depth=args.max_depth, max_leaf_nodes=args.max_leaves) x = np.array([traj[0] for traj in dataset]) y = np.array([traj[1] for traj in dataset]) weight = np.array([traj[2] for traj in dataset]) clf.fit(x, y, sample_weight=weight) # The current policy is the one that will # be used to sample the next trajectory policy = clf policies.append(clf) mean_reward = evaluate_policy(policy, env) rewards.append(mean_reward) # Retain the best policy over all runs best_policy = policies[np.argmax(rewards)] path = get_viper_path(args) print(f"Best policy:\t{np.argmax(rewards)}") print(f"Mean reward:\t{np.max(rewards):0.4f}")

While I was able to train a decision tree to play perfectly on both CartPole and ToyPong there are a few things to note:

Differences to DAgger

VIPER extends DAgger with the q-sampling trick, but it also changes the training schedule by only letting the oracle play in the first iteration while DAgger gradually reduces the participation of the oracle in each run. It is thus very easy to modify the above code to work like DAgger, and I was able to verify that both changes lead to better performance.

Verifying Correctness

We now have a DNN policy and a decision tree that both achieve a maximum reward on our ToyPong game. Now we want to verify that there is no edge case that would make our controller lose. This was the hardest part of the implementation and to show why it will help to have a look at the relevant section of the paper:

Excerpt from the paper

So the idea is that because the joint dynamics $f_{\pi}(s)$ are piecewise linear function we can use the linear programming algorithm to find exceptions to an equation that says that after at most $ t_{max} $ time steps we always end up in a safe state $ Y_0 $. To better understand the point about the piecewise linearity you can look at the figure below. Decision trees partition their input space into regions and each region is associated with a leaf node, i.e. action. The same can be said for the state dynamics which would for instance tell you that within the box the ball keeps moving while at each wall it bounces back. So if you come up with the right partitioning you can essentially write the joint dynamics as $f_{\pi}(s) = \beta_i^T s$ where each $\beta_i$ is a vector that encodes the next state of the system using the controller and system dynamics. 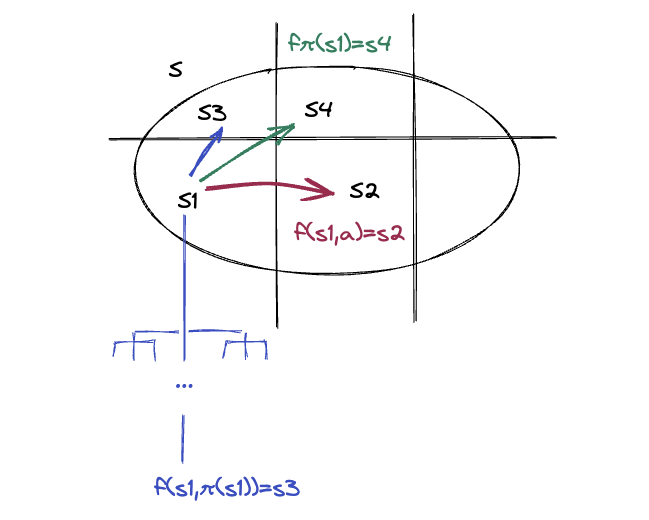Each $ \phi_t $ in the above program then captures the fact that if we are in one of the state partitions the transition to the next state will be governed by the corresponding $\beta_i$ A sharp-eyed reader might have already spotted a mistake in the $ \phi_t $ expression: While the paper specifies a disjunction over the state partitions this would make the expression trivially true because we are already not in all states but one. Instead, it has to be a conjunction which my experiments confirm. .

If the state dynamics are piecewise linear we can write the joint dynamics as a linear combination of the dynamics and the predicted action for each leaf node

But how do you programmatically build the correct partition and $ \beta $ from the decision tree? At first this question seemed stunningly hard until I realized that there is a straight-forward solution that was probably cut from the paper since it would have only complicated the equations. The trick is to split each expression in $ \phi_t $ into a controller and a system part. The controller part only controls $ s_t[0] $, i.e. the paddle, and the system equations, which have to be specified manually, the rest.

The full correctness check then comes out at less than 300 lines of code with comments. It uses the theorem prover z3 to show that the $ \neg \psi $ is unsatisfiable, i.e. there is no counter example to the safety property. Since my decision tree is considerably larger than the one in the paper the check takes about 38 seconds to run on my 2021 M1 MacBook Pro.

Reflections

The authors of the paper set out and deliver on the very ambitious goal of building a controller that does not only prioritize safety but in fact guarantees it. They also verify other safety properties such as stability and robustness on more environments that were not covered here. However, their verification approach requires the very strong assumption that we have the precise system dynamics as a piecewise linear function. In addition to that the environments are simple enough that we can train a perfect oracle policy that can be distilled into a decision tree. It is therefore an open question what the boundaries of this approach are, i.e. at what point is the difference in DNN policy and DT just big enough so that we cannot distill a perfect DT?

Overall, I greatly enjoyed studying and implementing this paper. The idea of extracting a DT from a DNN policy also has interesting implications for explainable RL agents (if the DT is small enough) and it would be interesting to see if this approach can be extended to more complex environments.